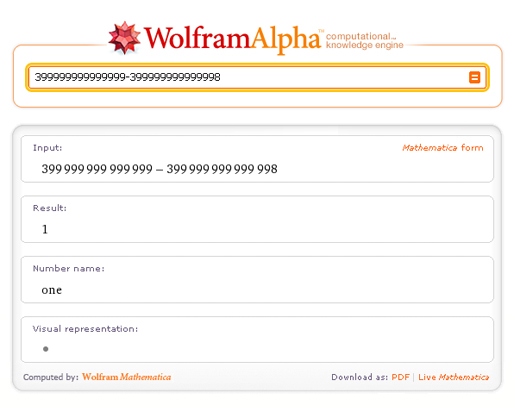
Para esas cosas existen buscadores más sofisticados como Wolfram Alpha, sino vean qué sucede con el coloso online cuando uno le plantea una resta tan simple.
Si lo quieren comprobar con sus propios ojos, ingresen aquí y aquí.
Comentarios
MIE, 3 / NOV / 2010
Google en matemáticas es tan bueno como un simio
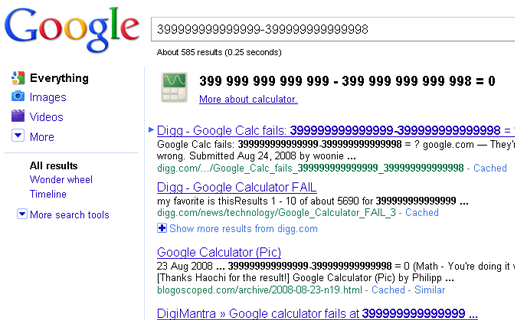Para esas cosas existen buscadores más sofisticados como Wolfram Alpha, sino vean qué sucede con el coloso online cuando uno le plantea una resta tan simple.
Si lo quieren comprobar con sus propios ojos, ingresen aquí y aquí.
[sarcasmo]Sí, google es una bosta yo cuando lo uso para restar mis centenares de billones de dólares y falta 1 dólar me pongo como loco!!!
Ni hablar de un amigo que trabaja para la nasa y hace esta misma cuenta en años luz CON GOOGLE…[/sarcasmo]
Ooo! no sabia eso e tenerlo en cuenta.
Más claro hechale agua con una mantisa completa!
PFloydRules, la mantisa de un número es la parte decimal.
Si vos tenés un número que representa un logaritmo (potencia de una base), la mantisa es la parte después de la coma hacia el dígito menos significativo.
Si calculamos el logaritmo de 1000 en base 10 (logaritmo es la potencia a la que debemos elevar una base para obtener el número original, para que la base^logaritmo sea igual a 1000. 10^3. (en este caso usamos base10, pero puede ser cualquier número R+)
entonces,
log(1000) = 3,000000… (y siguen los ceros)
porque 10^3 = 1000.
ese ,”000000…” es la mantisa, que en este caso se por tratarse de un número entero es =0.
Pero el log(135) = 2,1303337684950061166713448150409…
entonces “1303337684950061166713448150409” es la mantisa, la parte decimal de la potencia.
Si vamos elevando a la base 10 a las diferentes potencias tomando cada vez más dígitos:
10^2,13 = 134,89628825916536092479477181649
10^2,13033376 = 134,99999735933597519232949811066
10^2,13033376849500611667 = 134,9999999999999999995819656061
10 ^ 2,1303337684950061166713448150409 = 134,99999999999999999999999999973
vamos a ver que nos acercamos cada vez más al 135 original.
Eso es cambiar la precisión de la mantisa. Cuantos más decimales tomemos, mayor será la precisión del cálculo.
En la IEEE 754 están los detalles de la forma normalizada de representación binaria.
Abrazos
PFloydRules lo explicó perfectamente.
El genio que descubrió el “error” debería saber (o lo sabe y lo hizo de pura mala leche) que si pone valores capaces de superar la precisión necesaria de las variables que intervienen en el cálculo para lograr un resultado exacto obtendrá 0 como resultado.
Esto se debe al redondeo por truncamiento, y no importa el esquema de cálculo usado, ya que el espacio de memoria reservado para las variables tiene un límite físico.
Prueben con un número del orden de 10^22 en Bing, ó de 10^200 en Wolfram y van a obtener que a-(b-1)=0.
Ahora bien… Francamente…
Quizás la ‘calculadora de Google’ funciona sobre un viejo Pentium :p
http://es.wikipedia.org/wiki/Error_de_división_del_Intel_Pentium
aparte de pegarle un palazo a google esta nota e vieja vieja
25 de agosto del 2008 no lo digo de mala fe pero algo mas actual dentro de poco publican bug en la nueva vercion de win98se
ojo avizor el suyo!
Les dejo una traducción del quinto comentarista (thearssguy) de esta página:
http://digg.com/news/offbeat/Google_Calc_fails_399999999999999_399999999999998
“Las calculadoras como Google Calc usan aritmética de punto flotante para calcular estas operaciones.
En Google Calc se usa aritmética de punto flotante de doble presición.
La razón por la que Google Calc no puede diferenciar, por ej., 333333333333335 de 333333333333334 se debe a que en esa extensión los números tienen la misma representación binaria, porque se usan todos los dígitos significativos que la mantisa puede representar.
Lo más curioso es que en lugar de contar con una mantisa estándar de 52 bits (como define el IEEE 754), ésta tiene 4 bits menos, mientras que el exponente parece contar con todos los bits del estándar.
Así que la verdadera pregunta es: ¿Representación de punto flotante de 60 bits? WTF! (“que lo parió!” en argentino)”.
Ah, ¿y qué es la mantisa?:
http://es.wikipedia.org/wiki/Coma_flotante