El análisis de regresión es una técnica matemática que detecta pautas en el comportamiento de una variable, que luego pueden usarse para predecir nuevos valores de esta.
En este Informe USERS te presentamos las herramientas que ofrece Excel para efectuar este análisis.
Autor: Claudio Sánchez (sigue siendo SUPERPLANILLA!)
El problema
La tabla de la figura muestra los milímetros de lluvia caída a lo largo del año, junto con las ventas de paraguas de cada mes. Previsiblemente, las máximas ventas se dan en los meses más lluviosos.
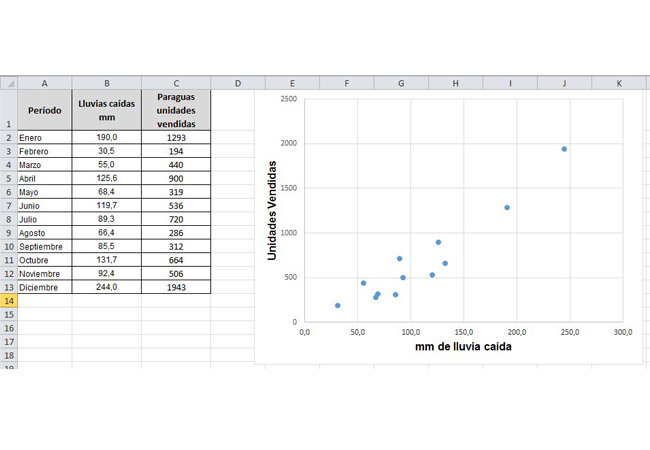
Milímetros de lluvia caída y venta de paraguas mes a mes.
Existen razones para pensar que esta relación no es casual: cuando llueve, la gente necesita paraguas y, si no tiene uno, debe comprarlo. Decimos que ambas magnitudes están correlacionadas: un aumento en la intensidad de las lluvias produce un aumento en la venta de paraguas. En este ejemplo, la cantidad de lluvia caída se llama “variable independiente” (llueve lo que llueve, y no hay nada que pueda hacerse para modificarlo). La cantidad de paraguas vendidos se denomina “variable dependiente”, porque depende de la anterior.
A la derecha de la figura están representados los datos de la tabla en un gráfico, que muestra algo interesante: los puntos se distribuyen, aproximadamente, en una línea recta. Por eso se dice que hay una relación lineal entre ambas variables. Teniendo en cuenta esta relación, puede usarse el pronóstico de lluvias para predecir la venta de paraguas. Esto es lo que hace el análisis de regresión: encuentra una relación entre los datos empíricos de dos variables y predice nuevos valores para la variable dependiente. Excel dispone de una batería de funciones que permiten realizar este análisis.
La función PRONÓSTICO
Supongamos que el Servicio Meteorológico anuncia una semana de lluvias con un total de 200 mm de agua caída. Queremos saber las ventas de paraguas que podemos esperar como consecuencia de esas lluvias. Para hacer el cálculo, recurriremos a la función PRONÓSTICO, tal como se observa en la siguiente figura.
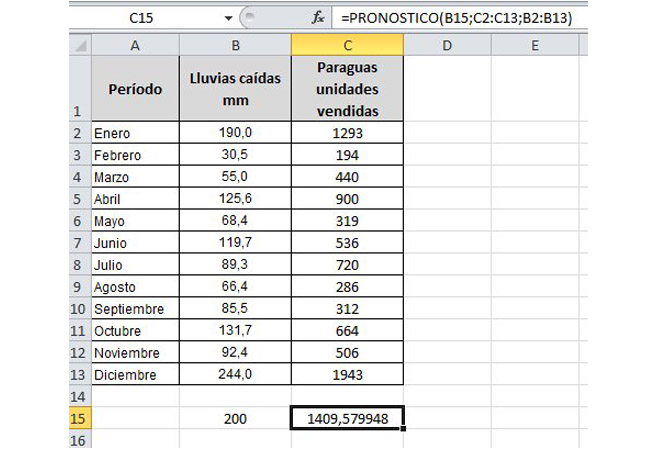
La fórmula de la celda C15 calcula las ventas de paraguas para los milímetros de lluvia caída indicados en B15.
La función PRONÓSTICO da el valor de la variable dependiente para un nuevo valor de la variable independiente. Tiene tres argumentos entre los paréntesis:
- El primero es el valor de la variable independiente para el que se quiere calcular la variable dependiente. En este caso, la cantidad de lluvia prevista por el Servicio Meteorológico.
- El segundo es un rango que contiene los valores conocidos de la variable dependiente.
- El tercero es un rango que contiene los valores conocidos de la variable independiente. Estos dos rangos deben tener la misma cantidad de filas.
Esta función se aplica a casos en los que existe una relación de proporcionalidad, o lineal, entre las variables, como en el ejemplo que estamos analizando.
Si llegaste hasta aquí en la explicación y entendiste la función PRONÓSTICO, ya sabes todo lo que tienes que saber para hacer regresión lineal con Excel. Veamos qué otras funciones de regresión puedes encontrar y qué hacer con ellas.
La función TENDENCIA
La función TENDENCIA es similar a PRONÓSTICO, pero permite calcular los valores de la variable dependiente para todo un rango de valores. En la siguiente figura se usa la función TENDENCIA para calcular los valores de venta de paraguas para todos los valores de lluvia caída del rango E2:E13.
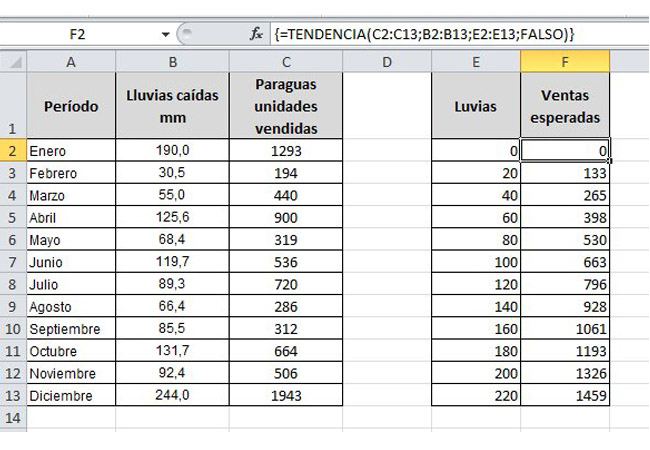
En el rango F2:F13 se usa la función TENDENCIA para calcular la venta de paraguas para los milímetros de lluvia caída indicados en E2:E13. Nótense las llaves que encierran a la función.
TENDENCIA es una función matricial. Eso significa que devuelve, no un dato individual, sino todo un rango. Además, debe ingresarse de manera especial:
- Selecciona el rango donde quieres calcular los valores de la variable dependiente. En el ejemplo, sería F2:F13.
- Escribe la función.
- Oprime la combinación CONTROL + SHIFT + ENTER.
La función calculará los cinco valores de la variable dependiente. En la barra de fórmulas la expresión aparecerá encerrada entre llaves, lo que revela que se trata de una función matricial. Esta función tiene cuatro argumentos entre los paréntesis.
- El primero es el rango de valores de la variable independiente
- El segundo es el rango de valores históricos de la variable dependiente. Estos dos rangos deben tener la misma cantidad de filas.
- El tercero es el rango de los valores de la variable independiente para los que se desea calcular los valores de la variable dependiente.
- El cuarto argumento es una constante lógica que indica el valor de la variable dependiente cuando la variable independiente es cero. Si el valor de este argumento es VERDADERO, la función supone que la variable independiente no necesariamente es cero. Si es FALSO, supone que es cero.
En el ejemplo indicamos el último argumento igual a FALSO: si no llueve, nadie comprará paraguas. Si se grafican los valores obtenidos con la función TENDENCIA, necesariamente se obtendrá una línea recta.
Continúa leyendo el Informe USERS 213 y aprende todos los conceptos y funciones relacionadas a las regresiones lineales y exponenciales
Informe USERS es una publicación digital semanal exclusiva para suscriptores de RedUSERS Premium, en ella analizamos en profundidad temas de actualidad en tecnología: tendencias, aplicaciones, hardware, nuevas tecnologías y más.
RedUSERS PREMIUM contiene cientos de publicaciones y puedes leerlas a todas, por una mínima cuota mensual SUSCRIBETE!












