Excel: Cómo crear un helecho Bransley o algoritmo iteractivo

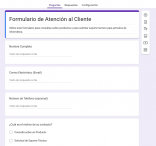
El algoritmo de este caso consiste en cuatro pares de fórmulas:

1. x_n+1=0 , y_n+1=0.16 * y_n
2. x_n+1=0.85 * x_n + 0.04 * y_n, y_n+1= -0.04 * x_n + 0.85 * y_n+ 1.6
3. x_n+1=0.2 * x_n – 0.26 * y_n, y_n+1= 0.23 * x_n + 0.22 * y_n+ 1.6
4. x_n+1=-0.15 * x_n + 0.28 * y_n, y_n+1= 0.26 * x_n + 0.24 * y_n+ 0.44

En estas fórmulas xn e yn representan las coordenadas del último punto dibujado y xn+1 e yn+1, las del próximo. Partiendo de un punto cualquiera del plano usamos estas fórmulas para obtener los siguientes puntos.

¿Cómo se decide cuál de los cuatro pares hay que usar en cada caso? Es una cuestión de probabilidad. Por ejemplo, supongamos que tenemos una ruleta con números del 1 al 100. La hacemos girar y, si sale el 100 aplicamos el primer par. Si sale un número entre 15 y 99, el segundo. Si sale uno entre 7 y 14, el tercero y si sale otro, el cuarto.

Para simular este efecto, usamos la función ALEATORIO, que genera un número de entre 0 y 1. En una hoja nueva, escribimos la función =ALEATORIO() en la celda [A2].

En las columnas [B] y [C] vamos obteniendo los pares de coordenadas x e y, comenzando con ceros en [B1] y [C1].

En [B2] escribimos esta triple condicional para obtener los valores de x:

=SI(A2>0,99;0;SI(A2>0,14;0,85*B1+0,04*C1;SI(A2>0,07;0,2*B1-0,26*C1;-0,15*B1+0,28*C1)))

En [C2] escribimos esta otra triple condicional para obtener los valores de y:

=SI(A2>0,99;0,16*C1;SI(A2>0,14;-0,04*B1+0,85*C1+1,6; SI(A2>0,07;0,23*B1+0,22*C1+1,6;0,26*B1+0,24*C1+0,44)))

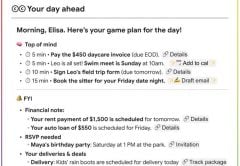
Para dibujar el helecho, usamos las columnas [B] y [C] para crear un gráfico de dispersión XY.